2018

Separating and predicting

Discrimination

  • Separating objects in an existing data set
  • Find which variables that best separate the \(g\) groups

Classification

  • Predict group membership for a new observation
  • Allocate new objects to known groups

Example 1: Iris Dataset

This famous (Fisher’s or Anderson’s) iris data set gives the measurements in centimeters of the variables:

  • Sepal Length (X1)
  • Sepal Width (X2)
  • Petal Length (X3)
  • Sepal Width (X4)

Example 1: Iris Dataset

load("_data/iris.train.Rdata")
head(iris.train)
   Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
61          5.0         2.0          3.5         1.0 versicolor
62          5.9         3.0          4.2         1.5 versicolor
63          6.0         2.2          4.0         1.0 versicolor
64          6.1         2.9          4.7         1.4 versicolor
65          5.6         2.9          3.6         1.3 versicolor
66          6.7         3.1          4.4         1.4 versicolor
  • Can we classify versicolor or virginica based on X-variables?
  • What’s the best method?

Iris Dataset: Pairs plot

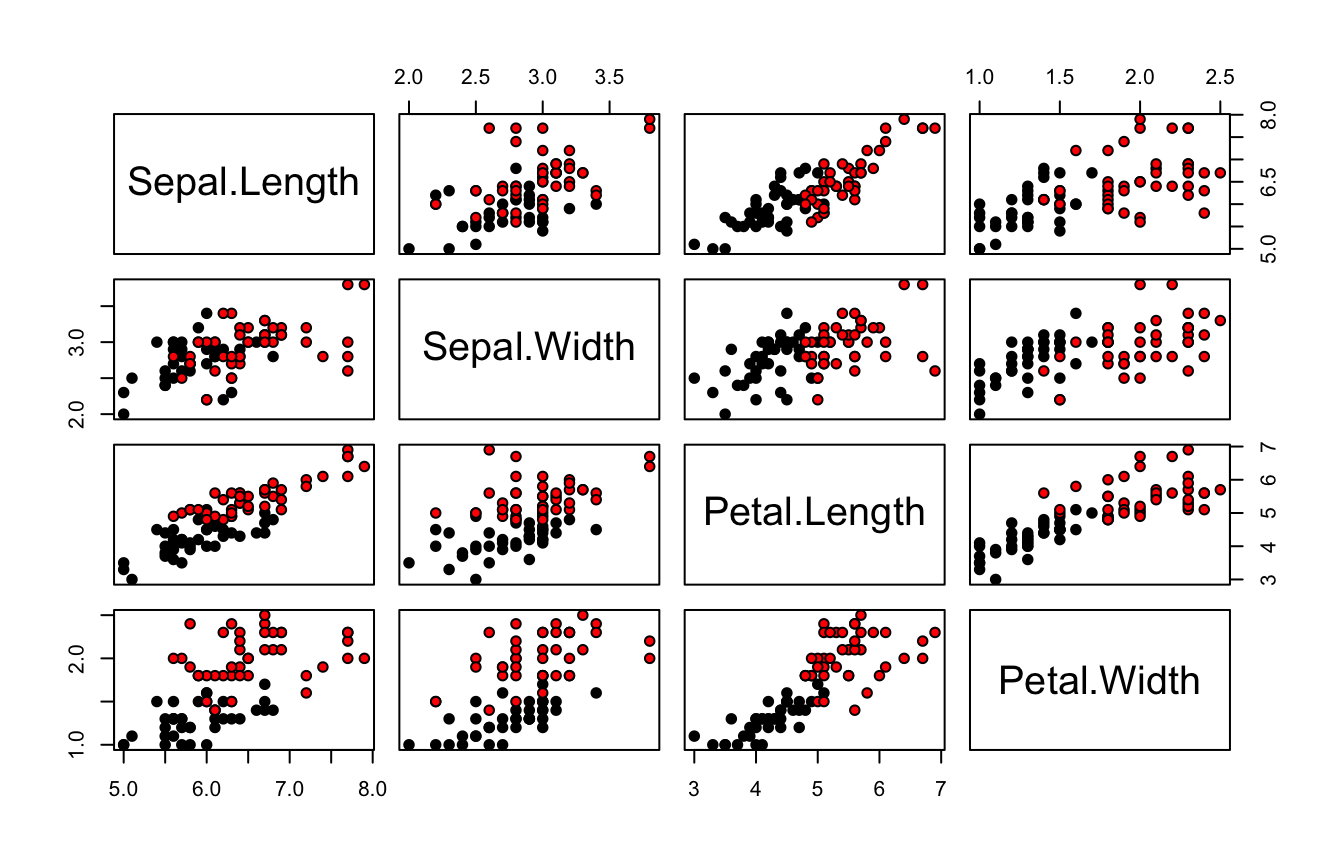
pairs(iris.train[, -5], bg = iris.train[, "Species"], pch = 21)

Example 2: Lizards

load("_data/Lizard.Rdata")
pairs(Lizard[, -4], bg = Lizard$Sex, 
      pch = 21, cex = 1.5)

variable Description
Mass Weight of Lizard (in grams)
SVL Snout-vent length (in mm)
HLS Hind limb span (in mm)


  • In addition to sex we have measured \(k = 3\) more variables on lizards as above.
  • Can we discriminate Sex on the basis of the body measures?

Example 2: Lizards

You must enable Javascript to view this page properly.

Lizard Dataset 

head(Lizard)
    Mass  SVL   HLS Sex
1  5.526 59.0 113.5   f
2 10.401 75.0 142.0   m
3  9.213 69.0 124.0   f
4  8.953 67.5 125.0   f
5  7.063 62.0 129.5   m
6  6.610 62.0 123.0   f

Finding decision regions

In descriminant analysis we search for decision regions for the \(g\) known groups (classes).

Regions \(R_1, R_2, \ldots, R_g\)

Univariate Descrimination

Bivariate discrimination

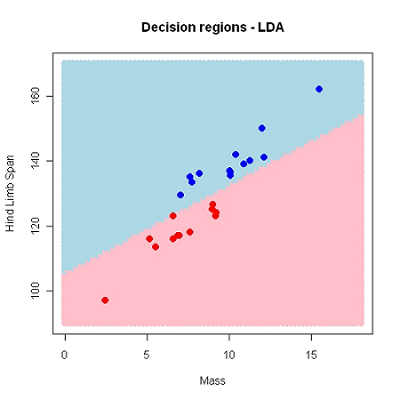
Using HLS and Mass as predictors \((k=2)\), we have used a linear decision border. This may also be non-linear.

Finding decision regions

You must enable Javascript to view this page properly.

Tri-variate discrimination

  • Using all variables \((k=3)\),
  • A linear discriminator is a flat plane in the 3D-space

Most probable group

  • Perfect discrimination/classification may not be possible.

  • The idea is to find decision regions \(R_1, R_2, \ldots, R_g\) that minimizes the probability of doing misclassification.

  • Intuitively we would allocate an observation to the group which is most probable given the observed value of the predictors

  • If, for example, the HLS of a new lizard is 130, it seems most probable based on previous data that the lizard is a male.

Bayes rule

Let \(P(c_i|x_1,\ldots, x_p)\) be the probability of class \(i\) given the observed variables.

Then by Bayes rule:

\[P(c_i|x_1,\ldots, x_p) \propto f(x_1,\ldots, x_p|c_i)p_i\]

where \(p_i\) is the a priori probability of observing an object from class \(c_i\) and…

\(f(x_1,\ldots, x_p|c_i)\) is the likelihood (“probability”) of the observed data given class \(i\).

A simple classification scheme

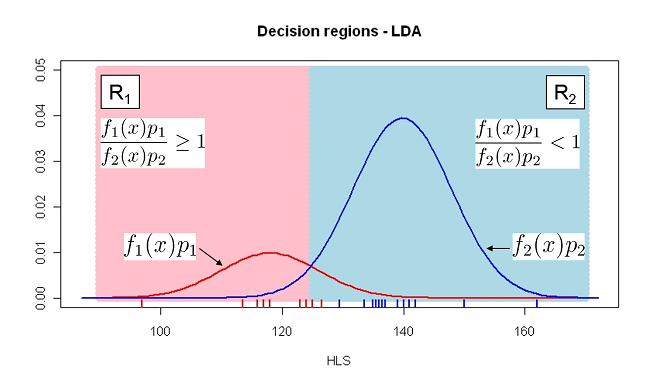
Allocate a new observation with observed variables \(x_1^*, x_2^*, \ldots x_p^*\) to the class which maximizes

\[f(x_1^*,\ldots, x_p^*)p_i\]

We need to estimate \(f(x_1^*,\ldots, x_p^*)\) from the training data and determine \(p_i\).

In linear discriminant analysis (LDA) we assume that \(f(x_1^*,\ldots, x_p^*)\) is a normal distribution, hence we must estimate the mean and (a common) variance for observations from each class.

Often we assume uniform prior: \(p_1 = p_2 = \cdots = p_g = 1/g\) .

Lizards example

Assume equal probabilities for females (\(c_1\)) and males (\(c_2\)) a priori: \(p_1 = p_2 = 0.5\)

Assume \(x_1\) = HLS is the only predictor.

From the data we estimate \(\mu_1\), \(\mu_2\) and common \(\sigma^2\) for both classes. Let \(f_1\) and \(f_2\) denote these two normal distributions.

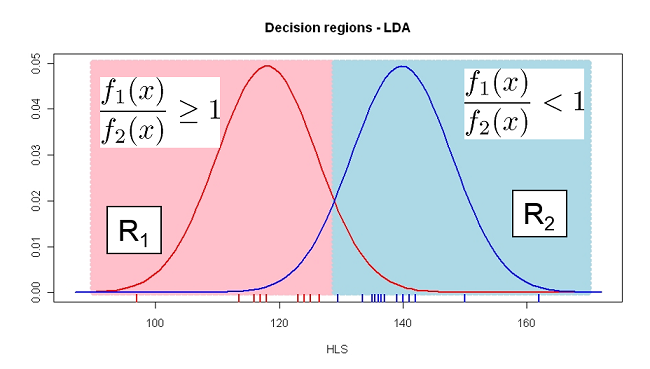
Classification rule: Classify a new lizard as female if

\[f_1(x_1^*)p_1 \geq f_2(x_1^*)p_2\]

or, alternatively if

\[\frac{f_1(x_1^*)p_1}{f_2(x_1^*)p_2}\geq 1\]

Visual representation

Linear Discreminent Analysis (LDA) in R

The fit is presented as a confusion matrix and accuracy of classification

library(MASS)
DAModel.1 <- lda(
  formula = Sex ~ HLS, 
  data = Lizard, 
  prior = rep(0.5, 2))
pred_mdl <- predict(DAModel.1)
    Mass  SVL   HLS Sex
1  5.526 59.0 113.5   f
2 10.401 75.0 142.0   m
3  9.213 69.0 124.0   f
4  8.953 67.5 125.0   f
5  7.063 62.0 129.5   m
6  6.610 62.0 123.0   f

R also returns the predicted classes (fitted) and \(P(c_i|x_1^*)\) also known as the posterior probability.

head(pred_mdl$posterior, 4)
           m          f
1 0.00590689 0.99409311
2 0.98750273 0.01249727
3 0.16418501 0.83581499
4 0.21513565 0.78486435
head(pred_mdl$class)
[1] f m f f m f
Levels: m f

Confusion Matrix and classification error

From the observed and predicted class of category Sex, we can construct a confusion matrix and calculate classification error. Remember the classification rule is, \[f_1(x_1^*)p_1 \geq f_2(x_1^*)p_2\]

Can you answer?

  • Can it classify with same accuracy for new observation?
  • Since this also depends on prior probability, how will it classify with different priors.

Confusion Matrix 

confusion(Lizard$Sex, pred_mdl$class)
            True
Predicted     m  f
  m          13  0
  f           0 12
  Total      13 12
  Correct    13 12
  Proportion  1  1

Accuracy 

N correct/N total = 25/25 = 1

Using different priors

If we assume males are more abundant: \(p_1 = 0.2\) and \(p_2=0.8\)

LDA in R using different priors

DAModel.2 <- lda(
  formula = Sex ~ HLS, 
  data = Lizard, 
  prior = c(0.8,0.2))
pred_mdl <- predict(DAModel.2)
confusion(Lizard$Sex, pred_mdl$class)
            True
Predicted     m          f
  m          13  2.0000000
  f           0 10.0000000
  Total      13 12.0000000
  Correct    13 10.0000000
  Proportion  1  0.8333333
N correct/N total = 23/25 = 0.92

The default choice prior

In R the default choice of prior is “empirical” which means that the priors are set equal to the group proportions in the data set

Hence, if there are \(n_i\) observations in group \(i\) and \(N = \sum_{i=1}^g n_i\) is the total observation number, then

\[\hat{p}_i = \frac{n_i}{N}\] This may be reasonable if one assumes that the sample sizes reflect population sizes.

Bivariate LDA

Quadratic discriminant analysis (QDA)

A Bivariate QDA - Decision regions

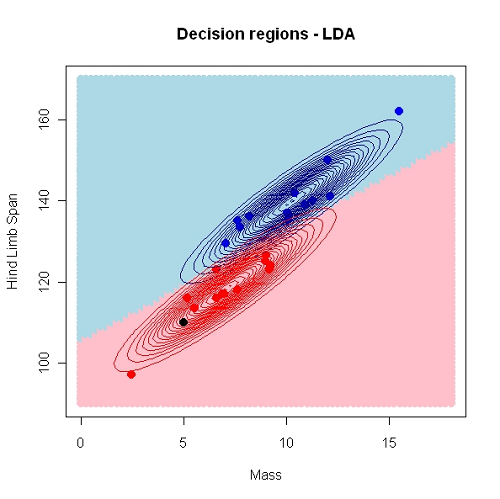
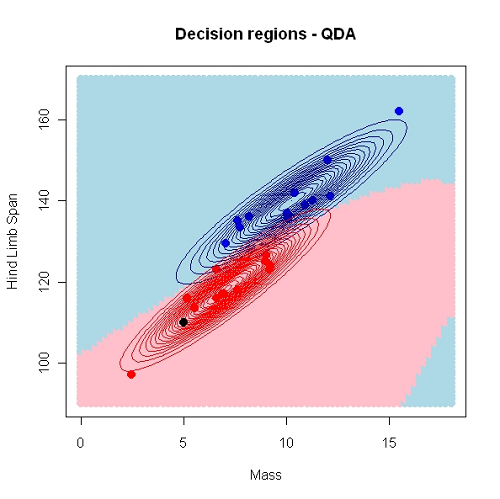
QDA differs from LDA in two ways:

  1. Class specific variances
  2. Non-linear decision borders

library(MASS)
QDA_model <- qda(
  formula = Sex ~ HLS, 
  data = Lizard, 
  prior = c(0.8,0.2))
pred_mdl <- predict(QDA_model)

Model selection/evaluation

  • We often want to compare the performance of different classifiers.

  • Many available statistics for this purpose, but we will consider the accuracy or the apparent error rate (APER)

  • The performance of a classifier may as we’ve seen be summarized in a confusion matrix

  • From the error rate, we can also compute the classification accuracy

Apparent Error Rate (APER)

Consider the confusion matrix as,

True
Male Female
Predicted
Male \(n_m/m\) \(n_m/f\)
Female \(n_f/m\) \(n_f/f\)
Total \(n_m\) \(n_f\)

\[ \text{APER} = \frac{n_m/f + n_f/m}{n_m + n_f} = \frac{\text{Total Incorrect}}{\text{Total Observation}} \]

Classification accuracy will be \(1 - \text{APER}\).

Example with R: SVL as predictor

DAModel.4 <- lda(
  formula = Sex ~ SVL, 
  data = Lizard, 
  prior = rep(0.5, 2))
pred_mdl <- predict(DAModel.4)
confusion(Lizard$Sex, pred_mdl$class)
            True
Predicted         m      f
  m          10.000  2.000
  f           3.000 10.000
  Total      13.000 12.000
  Correct    10.000 10.000
  Proportion  0.769  0.833

Probabilities of misclassification - APER

\[ \begin{aligned} P(\texttt{female | male}) &= \dfrac{3}{13} = 0.231 \\ P(\texttt{male | female}) &= \dfrac{2}{12} = 0.167 \end{aligned} \]

\[ \text{Apparent error rate (APER)} = \frac{3 + 2}{25} = 0.2 \]

Accuracy = \(1-\text{APER} = 0.8\)

Validation (Test-data or CV)

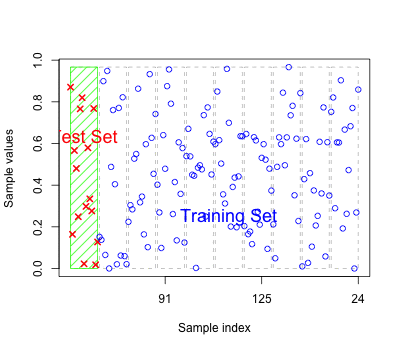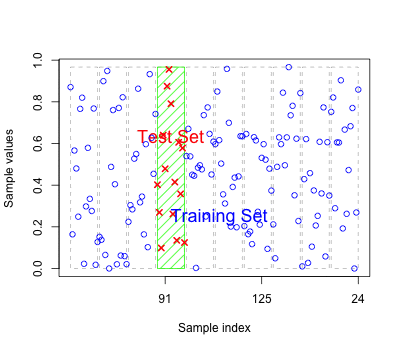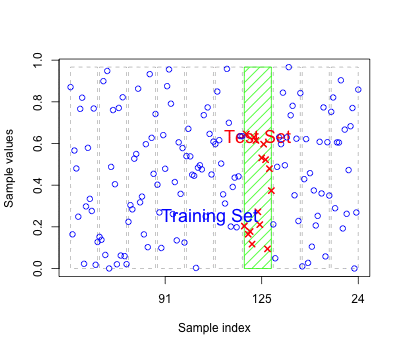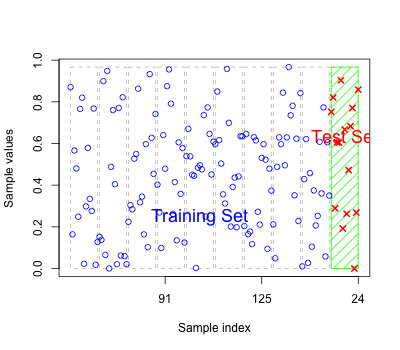
  • As for regression models the errors based on fitted values may reflect over-fitting

  • Should have new test data to predict to get an honest classification error.

  • Alternatively we can perform cross-validation

Types of Cross-Validation

  • K-fold cross-validation and

  • Leave-one-out (LOO) Cross-validation

LOO cross-validation: LDA with SVL as predictor

da_model <- lda(
  formula = Sex ~ SVL, 
  data = Lizard, 
  prior = rep(0.5,2),
  CV = TRUE)

confusion(Lizard$Sex, da_model$class)
            True
Predicted         m     f
  m          10.000  3.00
  f           3.000  9.00
  Total      13.000 12.00
  Correct    10.000  9.00
  Proportion  0.769  0.75

Typically, as seen here, the accuracy goes down, and the APER increases when new samples are classified.

APER (Error rate) 

N incorrect/N total = 6/25 = 0.24

Accuracy 

N correct/N total = 19/25 = 0.76

Thank You